Geometry and Graphics
Virtual Reality for Smart Cities
What if we could integrate the work we’ve done on traffic and buildings into one comprehensive digital twin? And how could such a digital twin be made more compelling to the general public? This project arose from a thought experiment and built on a project two of us did for HackSimBuild 2022.
- Wrote large parts of the book chapter discussing potential applications.
- Supported the prototype implementation through feedback and testing (credit for the heavy lifting of building it goes 100% to my colleague, Haowen!)

- Award for Best Demonstration at HackSimBuild 2022 for a project team of 5.
Ph.D. Thesis: Discrete Geometric Methods for Surface Deformation and Visualization
A lot of research I did as a Ph.D. student contributed to my thesis, but I had a few side quests as well. My main quest, however, was the modification of geometric surfaces under different constraints. (This gets math-y, you’ve been warned.)
Deformation that Preserves Total Gauß Curvature
In industrial surface generation, saving even a small of material in an individual piece can accumulate into substantial cost savings. Bending energy is one of the properties that are important in this context, and it can be measured using Gauß curvature. The goal of the deformation is to minimize (changes in) total Gauß curvature to minimize material cost and waste.
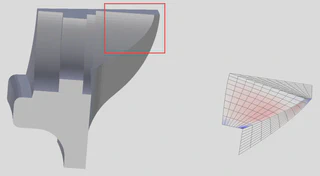
- Mathematical proof to determine the limits to the deformations.
- Performed case studies for a simple geometric form (helicoid) and a more complex machined part (fandisk), applying valid deformations and rendering the results (Matlab).
Efficient Deformation of Bézier Curves and Surfaces
Bézier curves are smooth parametric curves that can be defined by a small number of control points. Bézier surfaces are generated from meshes of control points using a similar method to create a smooth surface.
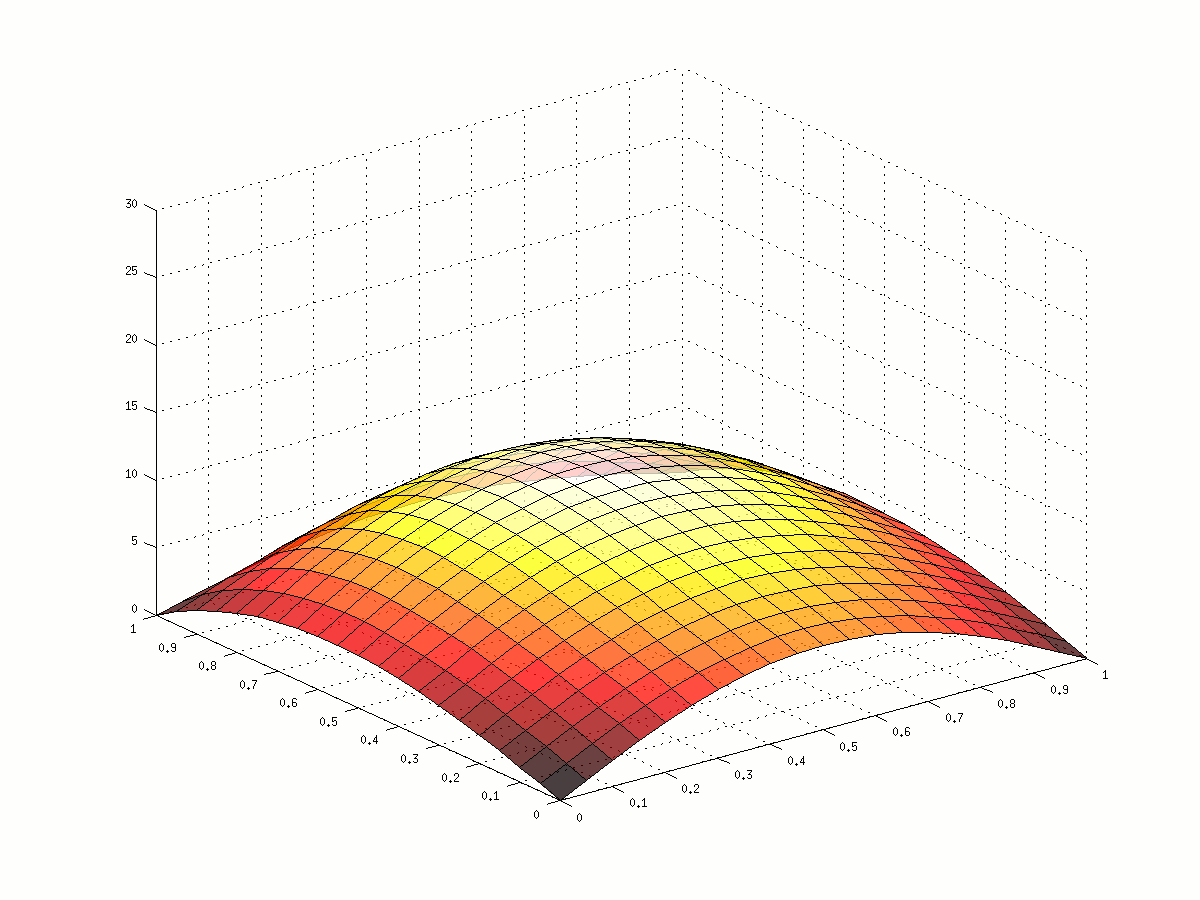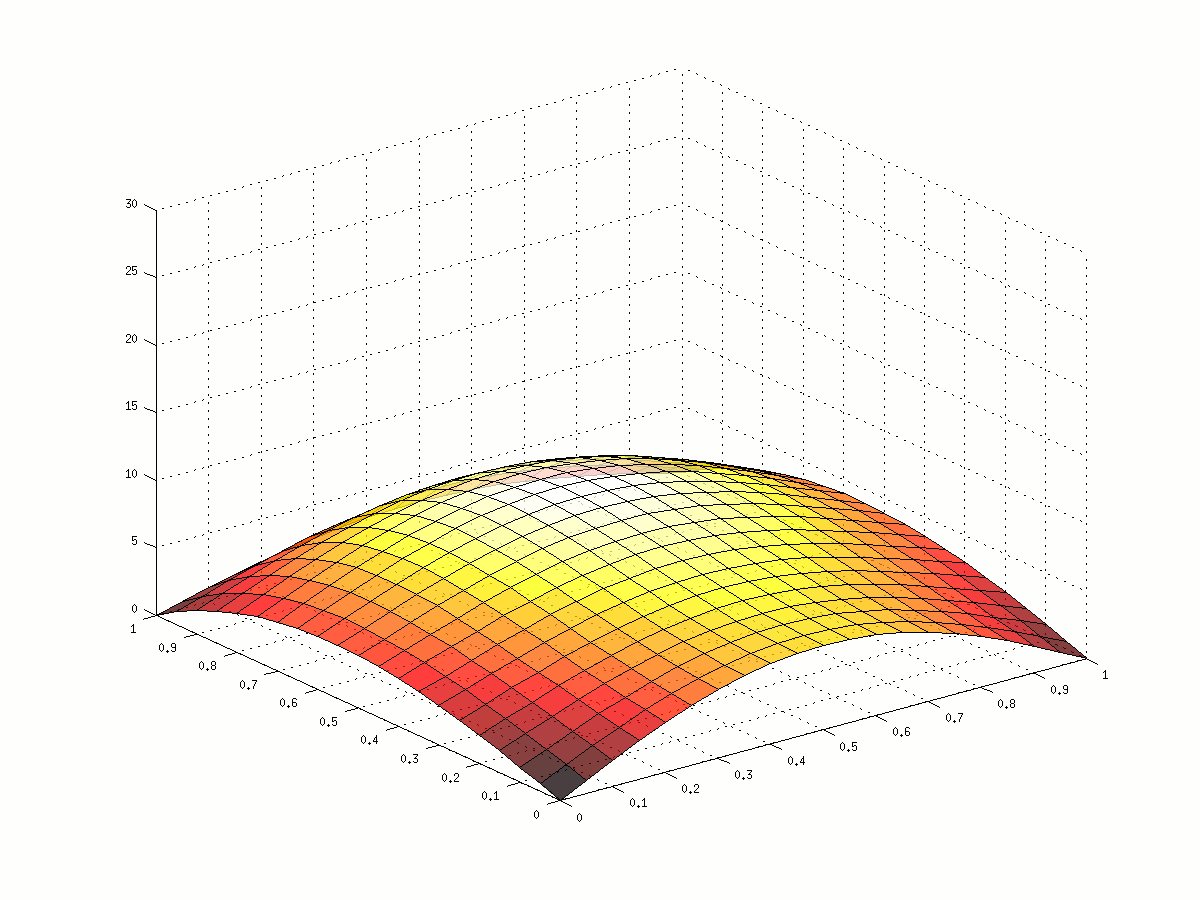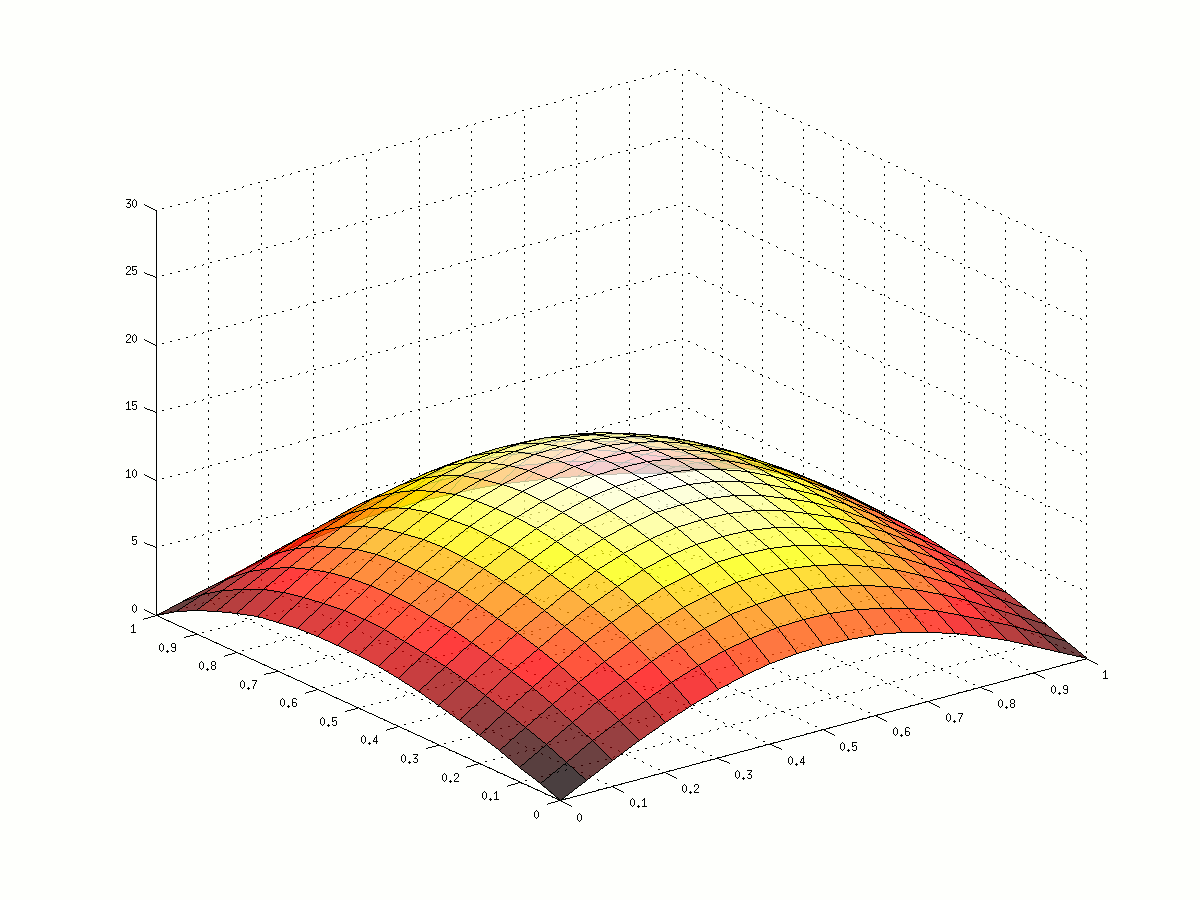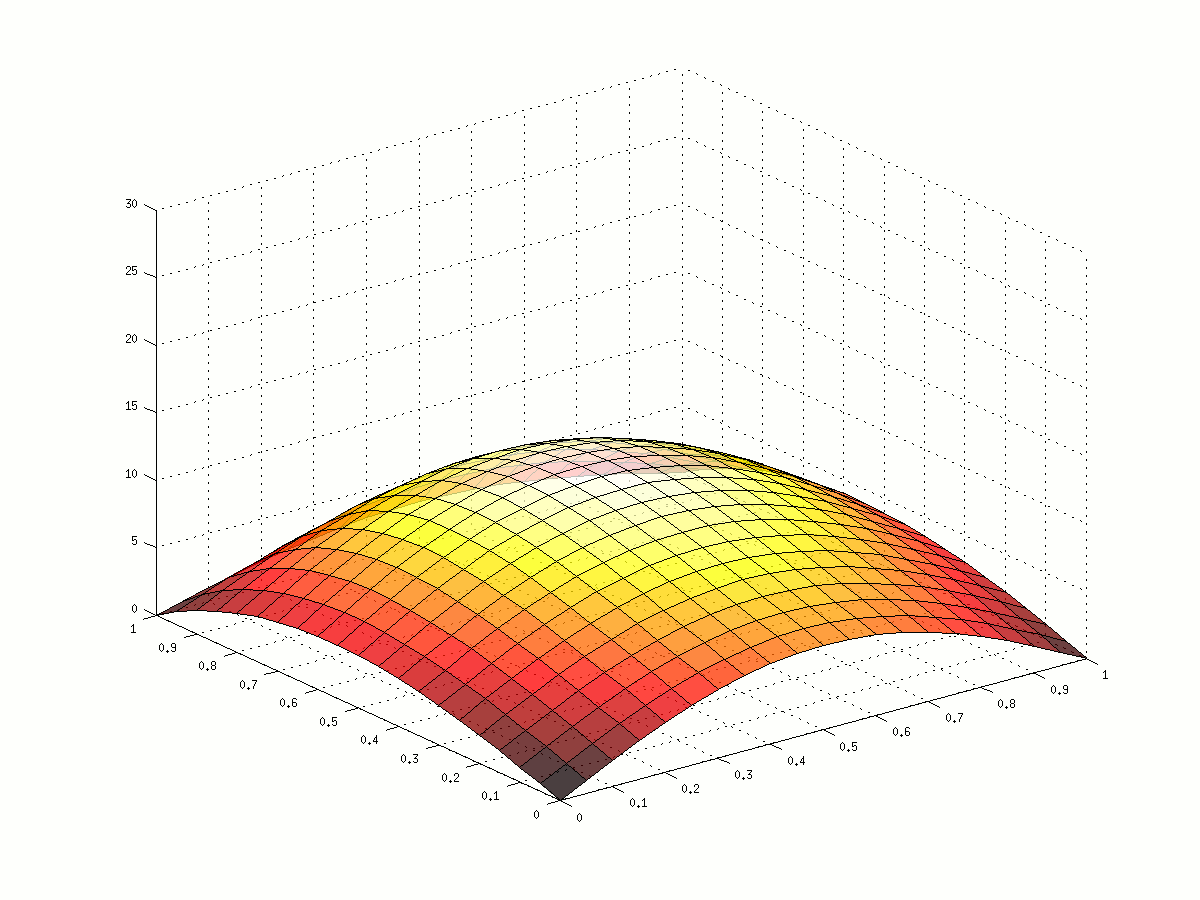
To deform the curve, you can take a lot of points and move them individually, but the resulting curve will no longer be smooth, and you will have to move a lot of points if you want it to look smooth. Instead, you could move the handful of control points and re-generate the curve in much less time. The question is: where do you move the points to achieve the desired outcome?
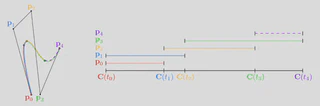
- Developed and compared four different approaches to deforming the control polygon: using the control polygon’s (discrete) normal, using normal at the curve point that matches the arc length of control point with respect to the polygon, using the normal vector that points from the curve to the control point, or using the normal vector for the curve point that’s closest to the control point.
- Developed a localized version that only allows nearby parts of the curve to affect the choice of normal.
- Evaluated feature preservation and complexity of all methods.

Optimizing Triangulations of Meshes after Deformation
In fluid simulations, the flow can be visualized by inserting particles and following them. One way to do this is to insert a flat surface with a fixed triangulation, and studying how this surface deforms over time. These surfaces are called time surfaces. Depending on the type of flow, these surfaces distort strongly, which results in a lot of very long and thin triangles. These are not desirable because their normal vectors are not well-defined (a line has no normal vector and the closer a triangle resembles a line, the worse the normal vector gets). Without well-defined normal vectors, the surfaces can’t be rendered nicely. To remediate this problem, I allowed the particles to move a little bit after each simulation time step to keep a more consistent sampling of the flow space. This is called particle relaxation.
- Developed a uniform particle relaxation which moves particles equally.
- Implemented a method to move particles by fitting a 3-dimensional surface (Coons patch) into nearby points, and moving the particle on this surface. This ensured that the surface does not shrink in this step.
- Developed a new relaxation criterion which considers the amount of distortion in parameter space, and counteracting this distortion (using the metric tensor).
- Developed an alternative relaxation criterion which considers the local Gauß curvature.
- Optimized the mesh after each step to preserve good triangle quality (i.e. good normals).
Side Quest: Geometric Reconstruction of Tokamak Data
For this internship project, I was tasked with visualizing Tokamak data from ELMFIRE fusion reactor simulation outputs which were provided by Aalto University, Finland.
The ELMFIRE simulation produced four slices through the Tokamak donut shape per time step, formatted in polar coordinates (rectangle).
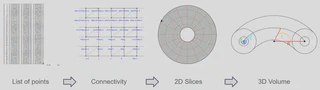
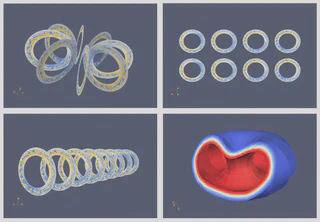
- Converted Tokamak simulation outputs from rectangles in polar coordinates (simulation output file format) to discs with holes (annullus) with appropriate triangulations (VTK).
- Transformed the discs to different layouts (flat, cylinder, torus).
- Interpolated intermediate slices.
- Constructed 3D volumetric data from discs and applied transformations to account for quasiballooning.
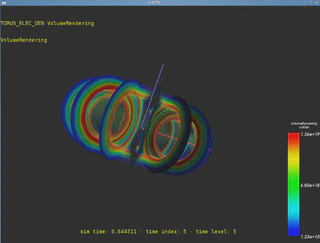
- Visualized 2D and 3D Tokamak data in ParaView in several different arrangements.
- Ported visualization to a VR Powerwall.
- Presented the results to a panel of German Aerospace and Aalto University staff.
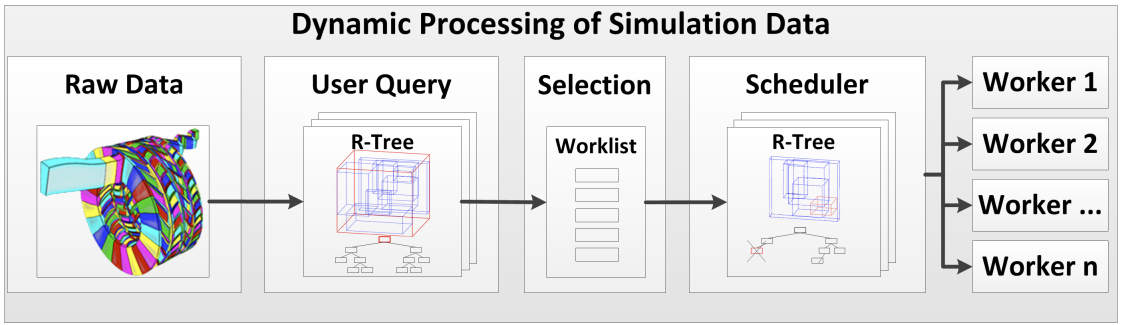
Side Quest: Dynamic Scheduling for Distributed Computations
This side quest was mostly my B.Sc. student’s main quest (thesis work), which I co-supervised with Prof. Hans Hagen (University of Kaiserslautern) and Markus Flatken (German Aerospace).
- Mentored my student in understanding the distributed data streaming and rendering pipeline.
- Discussed advantages and disadvantages of potential underlying data structures with my student.
- Guided my student in the development of a view-dependent dynamic scheduling system.
- Supervised the writing of the actual thesis, and contributed to the writing of a follow-up research paper.
- Deformations Preserving Gauss Curvature
- Surface Optimization for Time Surfaces
- Scheduling Computations for Big Simulation Data Workflows Paper about my mentee’s BSc thesis project.
B.Sc. thesis: Merging Triangulated Meshes
When designing a car, it’s a priority for the designers that the car doesn’t just look sleek, but that it is safe and comfortable for the people using it. To improve occupant safety, the German automotive industry has funded the development of RAMSIS, a system that uses 3D CAD manikins to simulate vehicle occupants and analyze the ergonomics and safety of vehicle interiors.
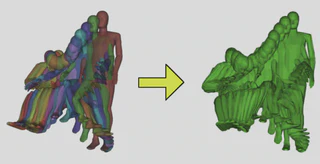
- Developed an algorithm to merge triangulated 3D meshes for RAMSIS, a 3D CAD simulation for vehicle occupants funded by the German automotive industry.
- Tested the algorithm on meshes of manikins which consisted of 2,700 triangles in 52 groups.
- Performed troubleshooting to determine which geometric properties the original meshes lacked and proposed a pre-processing step to fix the meshes and enable proper merging.
- Merged the meshes of manikins in multiple different poses to determine required space for safe and comfortable vehicle operation.