Deformations Preserving Gauß Curvature
Illustration of a Gauss frame for a surface X. It consists of the tangent plane which is spanned by the derivatives in u and v direction, and the normal vector at any given point.Abstract
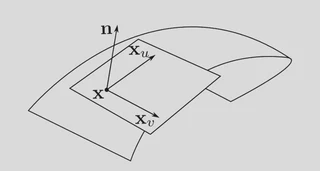
Surface prototyping generates a so-called masterpiece of a new product. Usually, a masterpiece is very similar to the final product, so only small modifications are supposed to be made. We present a linear deformation technique for this kind of modification, preserving total curvature of the masterpiece. The total curvature is directly connected to the topology of the surface, which is also directly related to the index sum of the singularities of a vector field acting on this surface. This means that our deformations modify the functionality of this surface in a controlled way.
Type
Publication
In Topological and Statistical Methods for Complex Data
